School of Engineering and Computer Science

XMUT103
Assignment 6: Graphs

Due 8 June , 19 pm

Download zip file of necessary code and data and extract it to an Assig6 folder (eg, in a COMP103 folder in your home folder). It should contain templates for the Java programs that will be marked.

Important note about the style of your code.

To submit

• BusNetworks.java (and Town.java if you modified it)
• MazeSearch.java

Do not rename these files.

Remember to submit all of these files. When you have submitted them, check that you can read the files listed on the submission page, and complete the submission process.

Part 1: Bus Networks (Weight: 50%)

For this question, you are to complete the BusNetworks program for analysing a proposed network of long-distance buses. The network consists of nodes for each of the towns in the region and links between pairs of towns that have a direct bus service.

The program reads data about the network from a file. The first line of the file has a list of the names of the towns in the region. Each remaining line has two names which are towns with a direct bus service between them.

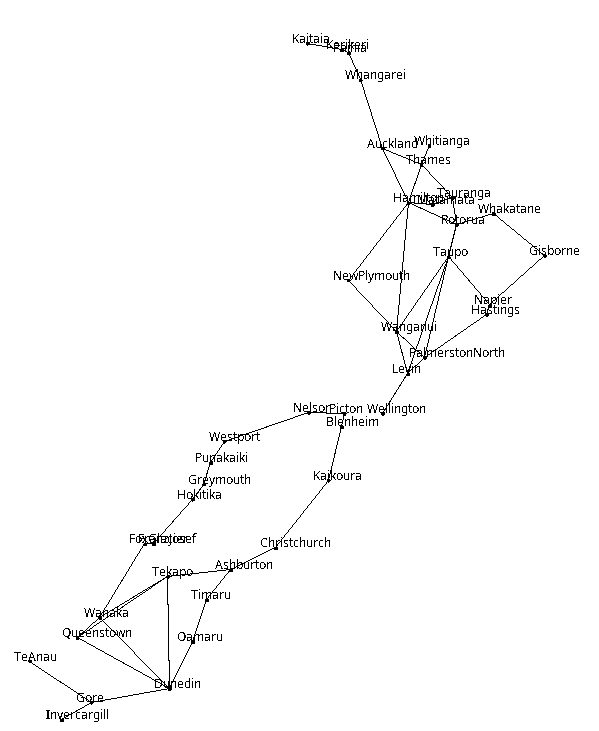
For example, the file "data-small.txt" file has just 7 towns and six direct bus services:

   Auckland Hamilton Napier NewPlymouth PalmerstonNorth Wellington Whanganui
   Auckland Hamilton
   Hamilton Napier
   Hamilton PalmerstonNorth
   NewPlymouth Whanganui
   Napier PalmerstonNorth
   PalmerstonNorth Wellington

There are two classes:

• The Town class (written for you) describes the nodes of the graph, with the name of the town and its set of neighbours (towns it has a direct bus service to).
• The busNetwork class that describes the bus network with all relevant functions you need to realise.

Core

• Complete the loadNetwork, printNetwork and finfRoute methods

The loadNetwork method is given the name of a file, and should read the data in the file, and construct a graph of the towns and their connections.

• The Town class (written for you) describes the nodes of the graph, with the name of the town and its set of neighbours (towns it has a direct bus service to).
• The busNetwork field should contain a map of all the towns in the network. The keys should be the names of the towns, and the values should be the Town objects. Note that the towns in the network may or may not be all connected.

There is a picture of the layout of the big busnetwork at the end of the assignment.

The printNetwork method should print out the network by printing one line for each town in the network, giving the name of the town, followed by its neighbours. Note, printNetwork does not need to traverse the graph - it can just use the collection of towns in busNetwork. For example, for the "data-small.txt" file, it should print (in any order)

The current network:
====================
Auckland-> Hamilton 
Hamilton-> Auckland PalmerstonNorth Napier 
Napier-> PalmerstonNorth Hamilton 
NewPlymouth-> Whanganui 
PalmerstonNorth-> Wellington Hamilton Napier 
Wellington-> PalmerstonNorth 
Whanganui-> NewPlymouth 

The findRoute method is passed a starting town and a destination town and should print out all the towns on a route (not necessarily the shortest route) between the starting town and the destination. It is OK (and simplest) to print the towns on the route in reverse order.
Hint: Use a recursive (post-order) depth first search with a helper method that has a visited set, and returns true if it found a route, and false if not.

Completion

• Complete the printReachable, and printConnectedGroups methods. You will need to construct a recursive "helper" method (findAllConnected method) for the printConnectedGroups method.

The printReachable method is passed a town and should print out all the other towns that can be reached from this town via the network. The towns should be printed in order of distance from the starting town, where distance is the number of stops along the way. Ie, it should print the towns that are direct neighbours of the town, then the towns that are two steps away, then three steps, etc. It should not print the starting town and it should not print any town more than once.
Hint: Use a breadth-first search, with a visited set.

The printConnectedGroups method should find all the connected sets of towns, and print each set on a separate line.
Hint: It may be useful to define and use a findAllConnected method to find all the towns connected to a particular town.

For example, for the "data-small.txt" file, there are two connected sets of towns that aren't connected to each other, so it should print:

Connected Towns
===============
Group 1: Auckland Hamilton PalmerstonNorth Wellington Napier 
Group 2: NewPlymouth Whanganui 

Challenge

• Display the network of towns graphically.
  (The file data-with-lat-long.txt contains the same network data as the data-big.txt, but in a different format (eg, it starts with the number of towns, followed by a line for each town and location), and with latitude/longitude information as well. (You will find this useful.)
  Ideally, it should let the user click on a town and highlight the part of the network (towns and links) that can be reached from that town.

---

Part 2: Maze Search (Weight: 50%)

The MazeSearch program creates mazes and then finds a path through the maze from any point the user clicks on to the goal square (shown in green). The part of the program that creates the maze is written for you. It creates a graph of MazeCells. Each MazeCell represents one square of the maze, and contains a collection of the neighbour MazeCells that are connected to it. You are to write the methods that search for paths through the graph of MazeCells to the goal MazeCell.

Core

Complete the exploreFromCell method which searches for a path from a given cell to the goal. As long as it hasn't visited the cell before, it should start by visiting the cell (using the cell.visit() method), colouring it yellow (using the cell.draw(Color.yellow) method), and pausing for a brief delay. It should then keep exploring from each of the neighbours. If it succeeds in finding a path through any of its neighbours, it should return true. If it cannot find a path through any of its neighbours, it should colour the cell red, and return false, to indicate that the cell was on a dead-end and it failed to find a path to the goal.

Your method should use a recursive depth-first search, but because the maze is a graph rather than a tree, it needs to mark each cell it goes to so that it can check that it does not visit it again later. Because you are only looking for one path, you don't need to "unvisit" the cells - just turning them red to indicate they were a dead end is enough.

The left hand image below shows a maze of size 10, where the user clicked in the top-left cell, and the program found a path to the goal. The yellow cells are the cells on the path, the blue cell is the goal, and the red cells are the cells that were on dead-end parts of the search.
Note that the search didn't find the shortest path (shown in the right hand image) - finding the shortest path is for the challenge.

Find a Path	Find Shortest Path

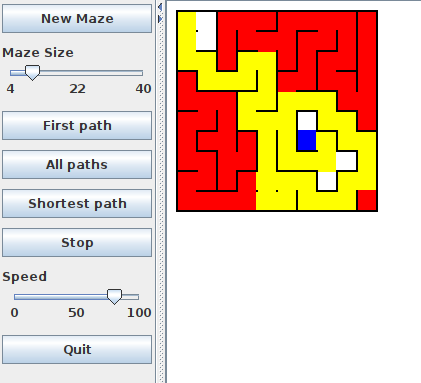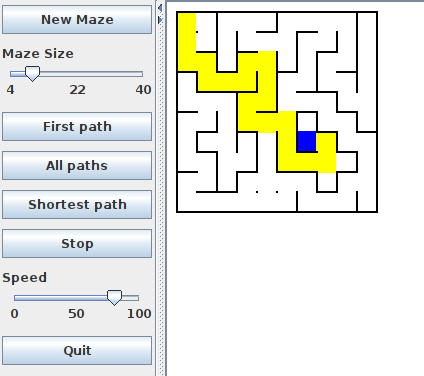Completion

Complete the exploreFromCellAll method which searches for all paths from the given cell to the goal. It should colour cells yellow (and pause briefly) as it visits them, but it should also unvisit them and colour them white after it has finished exploring the neighbours (successful or not). (This is so it can use the cell again in a different path).

Whenever it reaches the goal MazeCell, it should pause for 1000 milliseconds. (It may help to colour it blue before pausing and then colour it green again after pausing, just to highlight the fact that it found a path.) It should never try to explore past the goal cell.

Challenge

Complete the exploreFromCellShortest method which searches for the shortest path from the given cell to goal. It should not color the cells while it is searching. Instead, once it gets to the goal, it should colour all the cells on the path that got to the goal. To do this, it must have some way of recording the paths as it builds them, eg by recording the cell it came from every time it gets to a new cell.

The right hand image above shows the shortest path from the top left corner.

---

Appendix.

• network-layout.png: