Honest Signals
FIRST, have a look at this lovely intro by Carl Bergstrom - great stuff: http://octavia.zoology.washington.edu/handicap/honest_intro_01.html. Incidentally Veblen's book "Theory of the Leisure Class" (1899) can be read online, e.g. search for it on the VUW library and you'll see the link. Short list of examples where costly signaling might occur:- BEGGING FOR FOOD. Offspring signal hunger to parent (eg. birds: signal is chirping)
- DETERING PREDATORS
- prey signal escape ability to predators (eg. impala: stotting, babblers, meercats: alarm calls)
- prey signal poison/sting/other invisible defence to predators (eg. frogs, bees)
- INTIMIDATING RIVALS. Males signal fighting ability to each other (eg. deer: antlers, birds: food gifting)
- ATTRACTING MATES. Males signal 'quality' (genetic or life-history) to females (eg. peacocks: tails, humans: cars, haircuts, conversation)
- ATTRACTING VECTORS. Plants signal food to pollinators? (eg. flowering plants: colour)???
- WEALTH AND STATUS (subsumed by the above possibilities I think, e.g. attracting mates and intimidating rivals)
- conspicuous leisure (sports, tans)
- conspicuous consumption (cars, haircuts, lawns)
- higher education (Veblen: signals membership of leisure class) (Spense: signals prediction to employers).
A general model
MF: this is my attempt to get some clarity for myself about this, for kicking around with the SocialEvolutionReadingGroup Imagine two populations: signalers and receivers. Each signaler has a hidden quality (When is honest signaling an ESS?
CONDITION 1:Simplifications
This is (maybe) true, but too general to be of much use. One simplification is to focus on solutions that give "perfect" honest signaling in the sense that- We could ignore
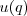 and focus on the direct costs of signaling, so that
and focus on the direct costs of signaling, so that 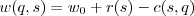 . We might anticipate (especially if we've read the literature...) that
. We might anticipate (especially if we've read the literature...) that 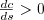 (ie. signals have a cost) but
(ie. signals have a cost) but 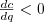 (that cost is lower for high-q individuals). But this alone isn't enough to give a "ridge" (see below).
(that cost is lower for high-q individuals). But this alone isn't enough to give a "ridge" (see below). Example 1: suppose we say the benefits are linear so that
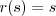 . That means the cost function can be anything for which
. That means the cost function can be anything for which 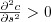 and
and 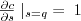 , so a candidate cost function is
, so a candidate cost function is 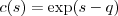 , i.e.
, i.e. 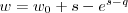 .
. Example 2: suppose we say the benefits are logarithmic,
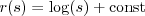 . That means the cost function can be anything for which
. That means the cost function can be anything for which 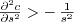 and
and 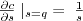 , so a candidate cost function is
, so a candidate cost function is  for example. That's a fitness of
for example. That's a fitness of 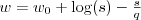 .
. - Alternatively we could make the direct costs simple and just dependent on the size of the signal (but not on
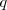 ), and instead focus on the ability
), and instead focus on the ability 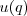 to make the most of the responses to one's signal. In that case the true "cost" of having low-q could be an inability to make the most of the potential benefits from signaling:
to make the most of the responses to one's signal. In that case the true "cost" of having low-q could be an inability to make the most of the potential benefits from signaling: 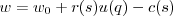 .
. Example 3:
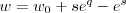 . This is Example 1, times
. This is Example 1, times 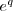 .
. Example 4:
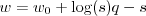 . This is Example 2, times
. This is Example 2, times 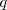 .
.
Examples
Summary table of the above examples:| Example | benefit | cost | in words |
|---|---|---|---|
| 1 | |
|
costs are exponential in signal strength, and exponentially worse if you're of low benefits scale linearly with signal strength |
| 2 | |
|
signals are costly, and REALLY costly if you are low quality benefits are logarithmic in signal strength: bigger and bigger signals bring less and less improvement |
| 3 | |
|
cost of signaling is exponential and their impact merely linear, but that impact can be exploited by an amount that's exponential in |
| 4 | |
|
cost of signaling is linear the direct impact of those signals is logarithmic, and is exploitable |
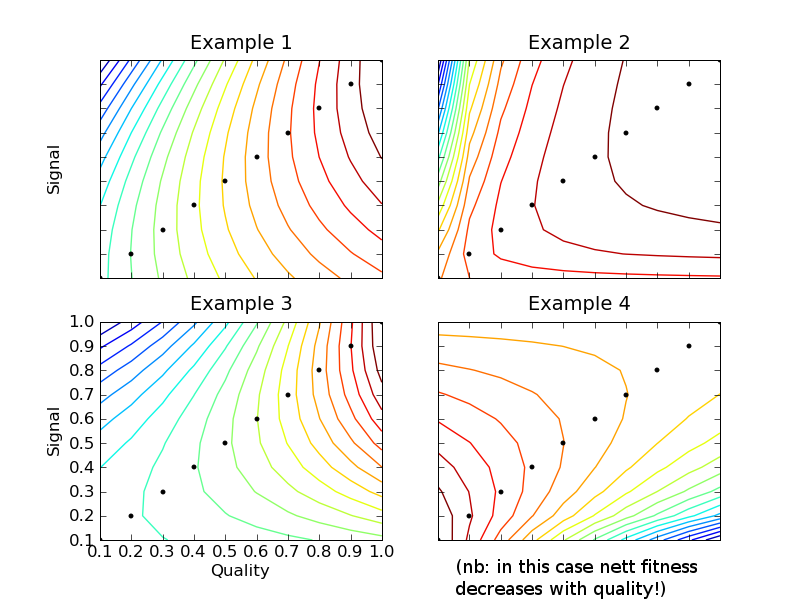 The fourth is kind of note-worthy, in that nett fitness actually goes down with quality. That sounds weird, but remember that "quality" here refers to the value of that individual's traits / genes to the receiver. Maciek pointed out this is close to the case of hungry offspring signaling to a parent.
The fourth is kind of note-worthy, in that nett fitness actually goes down with quality. That sounds weird, but remember that "quality" here refers to the value of that individual's traits / genes to the receiver. Maciek pointed out this is close to the case of hungry offspring signaling to a parent.
notes
- It's not really a ridge!! Surface's slope is actually monotonic in
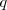 for all these examples (I think).
for all these examples (I think).
- Notice there are plenty of possibilities that involve costly signals, and have those costs greater for low-
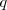 individuals, but which DON'T generate honest signaling. For example, with linear benefits
individuals, but which DON'T generate honest signaling. For example, with linear benefits 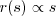 and costs
and costs 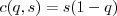 , the second derivative isn't negative so there's no maximum. There can't be any honest signalling equilibrium for such a system. So the costly, preferentially high-
, the second derivative isn't negative so there's no maximum. There can't be any honest signalling equilibrium for such a system. So the costly, preferentially high-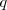 signal story is neither necessary (since direct costs don't have to be higher for low-
signal story is neither necessary (since direct costs don't have to be higher for low-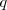 agents) nor sufficient (since you can have both yet still have no ridge).
agents) nor sufficient (since you can have both yet still have no ridge).
- Think about effect of noise in the q-to-s mapping, and costs of reception (requires model of receivers, which I've been avoiding). Aim to describe efficacy of cheap, noisy signals versus expensive accurate ones. "Speed dating".
- Think about one population, in which everyone is both a signaler and a receiver. I think this constrains the (joint) fitness equations a lot. But not sure how to combine the fitnesses from these two activities. Add? Multiply? Zogrify?
what about the receivers? and what is q, really?
The model has completely ignored receivers so far, simply assuming them to be paying attention to the signals and "rewarding" those with strong signals over those without. Denote fitness of the j-th receiver by (capital)sketch of signal-dependent coalition formation model (doesn't fly yet)...
Suppose the k-th receiver has "alliances" with signalers, whereSuper-simple version of all this obfuscation....
Maybe it's a red herring to worry so much about the details of surfaces. Maybe it's sufficient to talk about the simple game:| low |
high |
|
|---|---|---|
| signal | |
|
| no signal | |
|
-
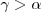 , and
, and
-
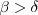
- high
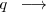 including this signaler in the group would be *good* for those group members with clout, and
including this signaler in the group would be *good* for those group members with clout, and
- low
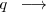 including this signaler in the group would be *bad* for those group members with clout
including this signaler in the group would be *bad* for those group members with clout
