Price's Equation
I like Gardner's 2008 summary especially. Must win the "Most dramatic final line" award for a scientific paper.
For heritable character values
z having fitnesses (number of offspring in next generation)
w the Price equation is
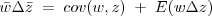
and it's often useful to write the covariance as a variance times a regression coefficient

:
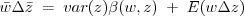
relation to Fisher's "Fundamental theorem"
If the heritable thing is "fitness" itself this is
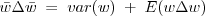
NOTE re Fisher: if we were to ignore the mutations (and all other "environmental" effects that might change the fitness of individuals directly) then the second term is zero and
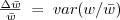
which is Fisher's theorem, i.e. a special case of the Price equation. The rate of increase in fitness at any time as a result of selection equals the variance of the (relative) fitness in the current population at that time.
note the "dynamic insufficiency"
To find the change in the mean (LHS) we need to know the current variance (1st term on RHS), so to understand the dynamics we need to know how the variance is changing as well. That's easy: use the same equation for

to get the rate of change of variance! But that requires a higher moment itself (variance of the variance), and so on...
For a dynamical model we'd need to have "moment closure": higher order moments would have to be expressed in terms of lower order moments. So Price's equation is described as lacking dynamic sufficiency. As it stands that's certainly true, but (according to Gardner et al 2007) the real issue is whether the system it is applied to enables this to be done.
relation to Frean and Baxter's famous never-submitting manuscript
-- marcus - 14 Jan 2009 Okay this is just a wondering for now.
The question: "Can we use the Price equation to derive the equilibrium distribution, e.g. in the B-D panmictic case?".
Price equation:
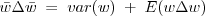
We've got a mutation process that does two things.
- It is what is generating the variance (the first term)
- It is unrelated to fitness and goes down more than up, so the second term is
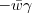 where
where 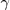 is the expected decrease in fitness resulting from mutations.
is the expected decrease in fitness resulting from mutations.
So we've got
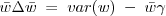
meaning that at equilbrium,
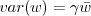
Is
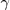
really 2 in our model? Since we know how we're generating the variance, can we do an approximate moment-closure (follow the recursion a step or two) to get an approximate
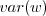
and hence nail
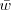
?
Ah, but ours is actually a different model so maybe this won't work... Us (actually Moran): births and deaths in a population with fixed N, no "generations" as such. Price: each generation, every individual (
i) produces

offspring (and dies). But is that a show-stopper, given pan-mictic population, and randomly chosen deaths? Seems pretty much the same to me.
musing off.
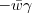 where
where 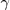 is the expected decrease in fitness resulting from mutations.
is the expected decrease in fitness resulting from mutations.


